By Danielle Zalesny
The method of Gelosia is used in the application of multiplication. As always in math, there are several ways to go about solving a problem. Today, we are accustomed to solving multiplication of multi-digit problems through the long multiplication method. However, another method widely was used, and even popular today, is the method of Gelosia. This method differs from long multiplication because it distinctly breaks down the multiplication and addition into two steps. It is also a lot less dependent on place value. This organizational method of multiplication also allows for numbers to be multiplied in a visual way, using a lattice-looking diagram. Today, in elementary school, this method, commonly known as the grid method or the box method, is usually shown as an introductory approach to solving multi-digit multiplication problems. Children go on to learn the traditional method of long multiplication once they are comfortable with this method. However, the method of gelosia proves to be extremely reliable. This method aims to show the steps of multiplication (multiply, carry, add) clearly and help people understand how numbers work.
As for the history of the method, Gelosia originated in India, as did much of our arithmetic. It first appeared in Hindu works. In India, this ancient multiplication approach was called the “quadrilateral.” From India, this method spread to ancient Chinese arithmetic in 1593. It also spread to Persia and the rest of the Arab world. It was especially popular in Arab and Persian works. In Arabia and Persia it was called the “method of the sieve” or “method of the net.”
To continue, this method eventually reached Italy, where it appeared in manuscripts in the 14th and 15 centuries. The method of gelosia appears in the first printed arithmetic book which was printed in Treviso, Italy in 1478. The name ‘gelosia’ was actually given to this method in Italy since the grid resembled the lattices or gratings that covered the windows of buildings. These gratings, which are called “gelosia” in Italian, were put on the windows of buildings in order to protect high class Italian women from the public view. In the old Byzantine custom of Italy, wives and daughters of Venetian nobles were kept sequestered in their homes. Another more popular name for this method is the Lattice method.
Furthermore, this method then reached Europe by way of Italy. It was introduced to Europe by Fibonacci, whose 1202 treatise Liber Abacii (Book of the Abacus) explained his work on arithmetic and number theory. The method remained popular for quite some time in Europe. It was widely accepted because of how organized it was. However, it eventually fell out of practice because it was difficult to print the lattice diagram with the printing methods used during the 15th century in Europe. Also, long multiplication took over as the dominant way of solving multiplication problems.
Additionally, the method of Gelosia is also how in 1617, John Napier’s, Napier’s bones evolved. Napier used an approach based on what is known today as the expansion of squares. Napier’s bones are a series of rods made from bone, wood, or ivory. The rods incorporate all of the possibilities in a Gelosia table. These rods are used to perform operations like multiplication and division, along with square and cube root problems.
As for the operation of this method, Gelosia is completed as follows:
First, a large square is drawn. The number of digits in each number you are multiplying corresponds to the number of squares you need to divide the large square into. For example, if one was multiplying 45 by 39, one would need to construct a large square divided into four squares. The two by two square box is the foundation for the grid-like method of Gelosia. The number of boxes varies depending on how many digits are in the numbers being multiplied. An example of a three by three box to multiply three digit numbers, as shown on the Wolfram MathWorld website, is shown below:
 |
| http://mathworld.wolfram.com/LatticeMethod.html |
|
Next, each square is diagonally split in half, with the diagonals extending outside the box. This crisscross look gives the appearance of a lattice looking diagram. To continue, the first number is written across the top, while the second number is written down the left hand side.
To begin finding a product, the first left upper hand box is looked at. The numbers on the corresponding row and column of the box are the ones that are multiplied. For instance, when multiplying the numbers in the diagram above, 948 by 827, the upper left hand box would correspond to the numbers 9 and 8. These two numbers are multiplied, and the partial product would be placed into the box. However, being diagonally spilt helps to establish place value in the box. In this case, 72 would be written with the 7 on the left side of the diagonal, representing the tens place and the 2 on the right side, representing the ones place. This same method is then performed for each of the remained boxes.
Once the multiplication is completed in each of the boxes, the operation of addition is performed. The diagonals in each box create diagonal stripes in the diagram. These diagonal stripes are added starting with the right one. The numbers that are included in the diagonal stripe are added together. The sum is written at the bottom of the diagonal stripe, outside the box. This is done for each diagonal stripe in the diagram. The sums of each stripe will be written from right to left across the bottom and then up along the left side of the box. The numbers, read from going down the left side and across the bottom, make up the product to the answer. The lattice arrangement of this method also effectively takes care of place value, with the right diagonal stripe being the ones column, followed by the tens, hundreds, etc.
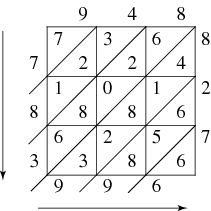 |
| From: http://mathworld.wolfram.com/LatticeMethod.html |
In some cases, like with multiplication problems with larger numbers, adding along the diagonal stripes will result in a number bigger than nine. In this case, the sum of the diagonal stripe, for instance if the sum was 13, is written with a three outside the box, and the one being carried over to the next diagonal stripe and added along with the numbers in that diagonal stripe.
Overall, this method, although the explanation seems complex and lengthy, is actually very simple to understand and use. The organizational element of the lattice arrangement allows for large multiplication problems to become a lot of small basic ones.
Interestingly, another aspect of this multiplication method that is extremely beneficial is the ability to multiply numbers with decimals. In this case, a problem involving a multi-digit decimal number, for example 12.3 X 1.24, allows for the decimal point position in the product to be easily determined. The process for solving problems with decimals is the same as multiplying whole multi-digit numbers, as explained above. The only difference is in the beginning when the numbers are written along the top and down the right side of the box. Although the digits are still written as before, the decimal point is drawn on one of the corresponding lines of the grid-like diagram. The two lines that match up the decimals, on the column and row, have a diagonal line in which they meet. This diagonal line becomes the point at which the decimal is placed in the product of the problem. This method successfully and easily locates the decimal position point in the product.
Overall, the method of Gelosia, is a simple and fascinating technique used to demonstrate the understanding of number sense. From ancient India all the way to the present day, this method allows users of it to visually focus on the steps of multiplication and turn complex multi-digit problems into smaller simpler multiplication problems.
Bibliography
Len, G. (n.d). Lattice Method—From Wolfram MathWorld. Wolfram MathWorld: The Web’s Most Extensive Mathematics Resource. Retrevied November 30, 2011, from http://mathworld.wolfram.com/Latticemethod.html



